การประมาณค่าตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัด(Correction Factor)สำหรับการทดสอบแท่งคอนกรีตซึ่งได้จากการเจาะ โดยวิธีการประมาณค่าในช่วงเชิงเส้น (Linear Interpolation) ด้วย Microsoft Excel(37,098 views)

ติงศักดิ์  เหลืองเจริญทิพย์

ฝ่ายห้องปฏิบัติการวิศวกรรม 2   ศูนย์เครื่องมือวิทยาศาสตร์และเทคโนโลยี  มหาวิทยาลัยเทคโนโลยีสุรนารี

Email: tingsak@sut.ac.th

1. บทนำ

การทดสอบความต้านแรงอัด (Compressive Strength) ของแท่งคอนกรีตรูปทรงกระบอกซึ่งได้จากการหล่อตัวอย่างคอนกรีตในแบบหล่อมาตรฐานนั้น  ส่วนใหญ่จะใช้แท่งทดสอบรูปทรงกระบอกขนาดเส้นผ่านศูนย์กลาง 150 มม. ความสูง 300 มม. ส่วนแท่งทดสอบซึ่งได้จากการเจาะจากโครงสร้างคอนกรีตที่ได้ก่อสร้างไปแล้วนั้น ต้องเป็นรูปทรงกระบอกและมีขนาดเส้นผ่านศูนย์กลางไม่น้อยกว่า 100 มม. และความยาวของแท่งทดสอบเมื่อยังไม่เคลือบปลายทั้งสองต้องไม่น้อยกว่าร้อยละ 95 ของเส้นผ่านศูนย์กลาง (วิธีทดสอบความต้านแรงอัดของแท่งคอนกรีต มอก.409-2525)

กรณีที่แท่งทดสอบซึ่งได้จากการเจาะมีส่วนสูงน้อยกว่า 2 เท่าของเส้นผ่านศูนย์กลาง  ต้องแก้ไขค่าความต้านแรงอัดที่คำนวณได้  โดยใช้ตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัด (Correction Factor) ตามตารางที่ 1  

ตารางที่ 1 อัตราส่วนความสูงต่อเส้นผ่านศูนย์กลาง  กับตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัด

(วิธีทดสอบความต้านแรงอัดของแท่งคอนกรีต มอก.409-2525)

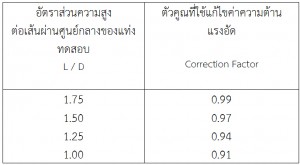
ในกรณีที่อัตราส่วนความสูงต่อเส้นผ่านศูนย์กลางของแท่งทดสอบ,(L/D) อยู่ระหว่างค่าที่ให้ไว้ในตาราง  จะต้องประมาณค่าของตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัด  ในที่นี้จะใช้วิธีการประมาณค่าในช่วงเชิงเส้น (Linear Interpolation) และเพื่อความสะดวกในการคำนวณผลการทดสอบ  จะใช้ฟังก์ชันต่างๆใน Excel Microsoft มาช่วยเพื่อให้การคำนวณเป็นไปโดยอัตโนมัติ  ตามวิธีการในหัวข้อต่อไป

2. การประมาณค่าตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัดโดยวิธีการประมาณค่าในช่วงเชิงเส้น

การประมาณค่าของตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัด  โดยวิธีการประมาณค่าในช่วงเชิงเส้นมีวิธีการดังต่อไปนี้

2.1 ป้อนข้อมูลผลการทดสอบความต้านแรงอัดแท่งคอนกรีต

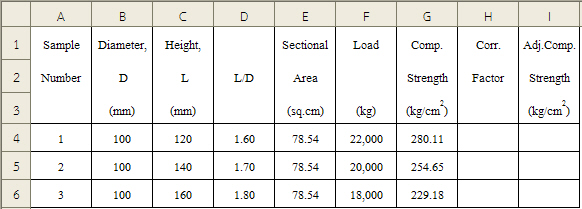
จากข้อมูลผลการทดสอบความต้านแรงอัดแท่งคอนกรีตรูปทรงกระบอกซึ่งได้จากการเจาะ จำนวน 3 ตัวอย่าง ป้อนข้อมูลลงใน Microsoft Excel พร้อมทั้งคำนวณ

-          อัตราส่วนความสูงต่อเส้นผ่านศูนย์กลางของแท่งทดสอบ,(L/D) ในเซล D4:D6

-          พื้นที่ภาคตัดขวางของแท่งคอนกรีต ในเซล E4:E6

-          ความต้านแรงอัดแท่งคอนกรีต ในเซล G4:G6

ตามรูปที่ 1

รูปที่ 1 ข้อมูลการทดสอบความต้านแรงอัดแท่งคอนกรีตซึ่งได้จากการเจาะ

จะพบว่าอัตราส่วนความสูงต่อเส้นผ่านศูนย์กลางของแท่งทดสอบ ,(L/D) ของตัวอย่างแท่งคอนกรีตทั้งหมดมีค่าน้อยกว่า 2 และอยู่ระหว่างค่าต่างๆที่ให้ไว้ในตารางที่ 1  ดังนั้นจะต้องแก้ไขค่าความต้านแรงอัดที่คำนวณได้  โดยต้องประมาณค่าของตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัดจากตารางที่ 1

2.2 การประมาณค่าในช่วงเชิงเส้น (Linear Interpolation)

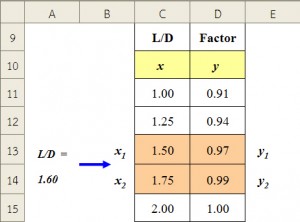
การประมาณค่าในช่วงเชิงเส้น (Linear Interpolation) สามารถแสดงได้ดังนี้ (รูปที่ 2)

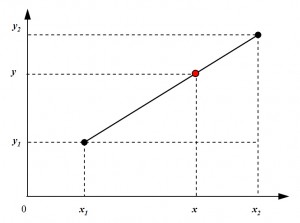รูปที่ 2 การประมาณค่าในช่วงเชิงเส้น (Linear Interpolation)

เมื่อทราบค่า (x₁, y₁) และ (x₂, y₂) แล้ว สามารถประมาณค่าของ  y  สำหรับ  x เมื่อ x₁ <= x <= x₂ จากสมการ

…………………………………..(1)

2.3 การประมาณค่าตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัด

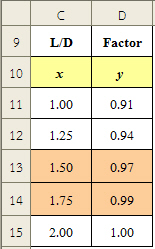
-  ป้อนข้อมูล อัตราส่วนความสูงต่อเส้นผ่านศูนย์กลาง  กับตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัด จากตารางที่ 1 โดยเรียงลำดับใหม่จากค่าน้อยไปหาค่ามาก  และเพิ่มข้อมูลอีก 1 ชุด ที่อัตราส่วนความสูงต่อเส้นผ่านศูนย์กลางเป็น 2.00 ตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัดมีค่าเท่ากับ 1.00  ตามรูปที่ 3

-  ตั้งชื่อค่าต่างๆของอัตราส่วนความสูงต่อเส้นผ่านศูนย์กลาง  โดยเลือกช่วงข้อมูล D11:D15 แล้วคลิกที่ Name Box ป้อนชื่อช่วงข้อมูลเป็น dataLD กด Enter ตามรูปที่ 4

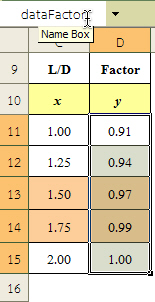
-  ตั้งชื่อค่าต่างๆของตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัด โดยเลือกช่วงข้อมูล E11:E15 แล้วคลิกที่ Name Box ป้อนชื่อช่วงข้อมูลเป็น dataFactor กด Enter ตามรูปที่ 5

ตัวอย่างการคำนวณของตัวอย่างแท่งคอนกรีต หมายเลข 1 ที่มีค่า  L/D = 1.60 (ตามรูปที่ 6) มีขั้นตอนดังต่อไปนี้

รูปที่ 6 ตัวอย่างการคำนวณของตัวอย่างแท่งคอนกรีต หมายเลข 1

(1)  หาตำแหน่งของค่า  L/D ที่มีค่าน้อยกว่าหรือเท่ากับ 1.60 โดย

คลิกเซล K4  ป้อนสูตร =MATCH(D4,dataLD)  จะได้ผลลัพธ์ในเซล K4  เป็น  3

กล่าวคือ ค่า L/D  ที่น้อยกว่าหรือเท่ากับ 1.60 จะอยู่ในตำแหน่งที่ 3 ของช่วงข้อมูล dataLD (เซล C11..C15)

(2) ตำแหน่งของค่า  L/D ที่มีค่ามากกว่า 1.60 จะเป็นตำแหน่งถัดไปคือตำแหน่งที่ 4 หรือ เท่ากับ  K4+1

คลิกเซล L4  ป้อนสูตร = K4+1 )  จะได้ผลลัพธ์ในเซล L4  เป็น  4

รูปที่ 7 แสดงตำแหน่งของค่า  L/D

(3) ที่ตำแหน่งของค่า  L/D ที่มีค่าน้อยกว่าหรือเท่ากับ 1.60 (ตำแหน่งของค่า L/D ที่ 3)

-          หาค่า  L/D โดยคลิกเซล M4  ป้อนสูตร =INDEX(dataLD,K4) จะได้ผลลัพธ์ในเซล M4  เป็น  1.50

-          หาค่าของตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัด โดยคลิกเซล O4 ป้อนสูตร =INDEX(dataFactor,K4) จะได้ผลลัพธ์ในเซล N4  เป็น  0.97

(4) ที่ตำแหน่งของค่า  L/D ที่มีค่ามากกว่า หรือเท่ากับ 1.60 (ตำแหน่งของค่า L/D ที่ 4)

-          หาค่า  L/D โดยคลิกเซล N4  ป้อนสูตร =INDEX(dataLD,L4) จะได้ผลลัพธ์ในเซล N4  เป็น  1.75

-          หาค่าของตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัด โดยคลิกเซล P4 ป้อนสูตร =INDEX(dataFactor,L4) จะได้ผลลัพธ์ในเซล P4  เป็น  0.99

(5) จะได้ค่า x₁,x₂,y₁,y₂ ตามสมการที่ 1 และสามารถหาค่า y ที่  x = 1.60  โดย

คลิกเซล Q4  ป้อนสูตร =O4+(D4-M4)*(P4-O4)/(N4-M4) จะได้ผลลัพธ์ในเซล Q4  เป็น  0.9780

ซึ่งเป็นค่าตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัดโดยวิธีการประมาณในช่วงเชิงเส้นตามต้องการ

(6) สามารถคำนวณค่า y ที่  x = 1.60  โดยใช้ฟังก์ชัน TREND  ที่มีใน Microsoft Excel  ได้โดย

คลิกเซล R4  ป้อนสูตร =TREND(O4:P4,M4:N4,D4) จะได้ผลลัพธ์ในเซล R4  เป็น  0.9780 เช่นเดียวกัน

(7) คัดลอกเซล K4..R4 มาที่เซล K5..R5 และ K6..R6

จะได้ค่าตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัดของตัวอย่างทั้งสาม ตามรูปที่ 8

รูปที่ 8 ผลการคำนวณค่าตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัดของตัวอย่างทั้งสาม

(8) คำนวณค่าความต้านแรงอัดที่ปรับแก้ โดย

-          คลิกเซล H4  ป้อนสูตร =Q4  จะได้ผลลัพธ์ในเซล H4  เป็น  0.9780

-           คลิกเซล I4  ป้อนสูตร =G4*H4  จะได้ผลลัพธ์ในเซล I4  เป็น  273.95

-          คัดลอกเซล H4..I4 มาที่เซล H5..I5 และ H6..I6 จะได้ค่าตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัดและค่าความต้านแรงอัดที่ปรับแก้แล้วของตัวอย่างทั้งสาม ตามรูปที่ 9

รูปที่ 9 ผลการคำนวณความต้านแรงอัดที่ปรับแก้แล้ว

3. สรุป

วิธีการประมาณค่าตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัดสำหรับการทดสอบแท่งคอนกรีตซึ่งได้จากการเจาะ  โดยใช้โปรแกรม Microsoft Excel ตามที่ได้แสดงมาแล้วนั้น สามารถนำไปประยุกต์ใช้ในงานอื่นๆได้ เช่น การประมาณค่าสัมประสิทธิ์ของโมเมนต์สำหรับแผ่นพื้นสองทางในการออกแบบพื้นคอนกรีตเสริมเหล็ก การประมาณค่าความหนาแน่นของน้ำที่อุณหภูมิและความดันบรรยากาศที่ทำการทดลองจากตารางอ้างอิง เป็นต้น

อนึ่ง ตารางอัตราส่วนความสูงต่อเส้นผ่านศูนย์กลางกับตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัดที่ใช้ในตัวอย่างการคำนวณตามตารางที่ 1 นั้น  อ้างอิงจากมาตรฐานผลิตภัณฑ์อุตสาหกรรม วิธีทดสอบความต้านแรงอัดของแท่งคอนกรีต มอก.409-2525  ซึ่งจะมีความแตกต่างอยู่บ้างจากตารางอัตราส่วนความสูงต่อเส้นผ่านศูนย์กลางกับตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัดตาม Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens: ASTM C39/C39M – 10 เนื่องจาก มอก.409-2525 นั้น กำหนดขึ้นตาม ASTM C39-72 ดังนั้น จึงต้องเลือกใช้ตารางอัตราส่วนความสูงต่อเส้นผ่านศูนย์กลางกับตัวคูณที่ใช้แก้ไขค่าความต้านแรงอัดตามมาตรฐานการทดสอบที่ใช้ในการทดสอบ

********************************************

เอกสารอ้างอิง

สำนักงานมาตรฐานผลิตภัณฑ์อุตสาหกรรม. (2543). มาตรฐานผลิตภัณฑ์อุตสาหกรรม วิธีทดสอบความต้านแรงอัดของแท่งคอนกรีต มอก.409-2525. พิมพ์เพิ่มเติมครั้งที่ 4. กรุงเทพฯ.

American Society for Testing and Materials. ASTM C39/C39M – 10  Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens: . Philadelphia, PA : ASTM.