การปรับแก้ Load-Penetration Curve ของการทดสอบ CBR โดยใช้โปรแกรม Microsoft Excel(82,404 views)

ติงศักดิ์  เหลืองเจริญทิพย์

ฝ่ายห้องปฏิบัติการวิศวกรรม 2   ศูนย์เครื่องมือวิทยาศาสตร์และเทคโนโลยี  มหาวิทยาลัยเทคโนโลยีสุรนารี

Email: tingsak@sut.ac.th

1. บทนำ

การทดสอบตัวอย่างดินด้วยวิธี CBR (California Bearing Ratio ตามมาตรฐาน ASTM D-1883 และ AASHTO T-193) เป็นการเปรียบเทียบหน่วยแรง (unit load) ต้านทานแรงกดของตัวอย่างดินต่อหน่วยแรงต้านทานแรงกดของหินคลุกมาตรฐานบดอัด ซึ่งวิธีการทดสอบโดยสังเขปประกอบด้วยการกดตัวอย่างดินด้วยหัวกดมาตรฐาน (Penetration Piston) ด้วยอัตราการกด 0.05 นิ้ว/นาที (รูปที่ 1) บันทึกค่าแรงกด (Load) ที่ระยะจม (Penetration) ต่างๆของหัวกดตามมาตรฐานกำหนด

พล็อตเส้นโค้งผลการทดสอบระหว่างค่าหน่วยแรงกด (Unit load) กับ ระยะจม (Penetration) ของหัวกด (Load-Penetration Curve) ตามรูปที่ 2 เพื่อหาค่าหน่วยแรงกด ที่ ระยะจม 0.1 นิ้ว และ 0.2 นิ้ว นำไปคำนวณค่าเปอร์เซ็นต์ CBR ของแต่ละค่าพลังงานการบดอัด (Compaction effort) จากสมการต่อไปนี้

	ที่ Penetration 0.1 นิ้ว		(1)
	ที่ Penetration 0.2 นิ้ว		(2)

รูปที่ 1 การทดสอบดินด้วยวิธี CBR

 รูปที่ 2 Correction of Load-Penetration Curves         
(ASTM D 1883)

ตามปกติ Load-Penetration Curve จากการทดสอบควรมีลักษณะโค้งคว่ำ (concave downward shape) และผ่านจุดกำเนิดดังกราฟเส้นบนสุดตามรูปที่ 2  โดยความชันของเส้นโค้งจะมีค่ามากที่สุดที่จุดเริ่มต้นและมีค่าลดลงไปเมื่อค่า penetration มีค่าเพิ่มขึ้น แต่ในบางกรณี Load-Penetration Curve จากการทดสอบที่ได้ส่วนต้นของเส้นโค้งอาจมีลักษณะเป็นโค้งหงาย (concave upward shape) ดังกราฟเส้นกลางและล่างสุดตามรูปที่ 2 โดยอาจเกิดได้จากการที่ผิวหน้าของวัสดุที่ทดสอบไม่ปกติหรือจากสาเหตุอื่นๆ ซึ่งจะต้องทำการปรับแก้กราฟโดยการลากเส้นตรงให้สัมผัสกับเส้นโค้งที่ตำแหน่งที่มีความชันมากที่สุดให้ไปตัดกับแกนนอน (penetration) และใช้จุดตัดดังกล่าวเป็นจุดกำเนิดใหม่ของกราฟ ตามรูปที่ 2

การปรับแก้ Load-Penetration Curve ตามที่กล่าวมานั้นสามารถใช้โปรแกรม Microsoft Excel ช่วยในการคำนวณปรับแก้ได้ตามวิธีการในหัวข้อต่อไป

2. การปรับแก้ Load-Penetration Curve

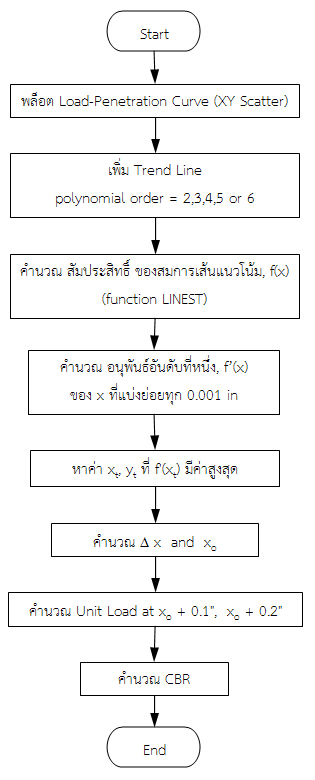
การปรับแก้ Load-Penetration Curve มีขั้นตอนโดยสังเขปดังต่อไปนี้

รูปที่ 3 ขั้นตอนการปรับแก้ Load-Penetration Curve

2.1 พล็อต Load-Penetration Curve (XY Scatter)

จากตัวอย่างข้อมูลการทดสอบ CBR ที่การบดอัด 12 ครั้ง/ชั้น ตามรูปที่ 4 พล็อตกราฟผลการทดสอบระหว่างค่าหน่วยแรง กับ ค่าระยะจมของหัวกด โดยพล็อตเฉพาะจุดข้อมูลเท่านั้น (XY Scatter) ตามวิธีการดังนี้

- เลือกช่วงข้อมูล A4:B14 ตามรูปที่ 4

รูปที่ 4 ข้อมูลการทดสอบ CBR

- คลิกปุ่ม Chart Wizard

- เลือกแท็บ Standard Types แล้วเลือก

Chart type: XY (Scatter)

Chart sub-type: Scatter. Compares pairs of values

ตามรูปที่ 5

รูปที่ 5 เลือกประเภทของกราฟ

- คลิกปุ่ม Next ไปที่ Step 3 of 4 – Chart Options ตามรูปที่ 6

กำหนดชื่อของกราฟ (Load-penetration Curve) แกนตั้ง (Unit Load) และแกนนอน (Penetration)

แล้วคลิก Finish เพื่อให้ได้กราฟตามรูปที่ 7

รูปที่ 6  Load-Penetration Curve (XY Scatter)

รูปที่ 7 Load-Penetration Curve (XY Scatter)

2.2 เพิ่มเส้นแนวโน้ม (Trend Line)

เพิ่มเส้นแนวโน้ม (Trend Line) ให้ชุดของข้อมูล ตามวิธีการดังนี้

- คลิกเมาส์ขวาที่จุดใดจุดหนึ่งของชุดข้อมูล และคลิกที่คำสั่ง Add Trendline ตามรูปที่ 8

รูปที่ 8 เรียกคำสั่ง Add Trendline…

- เลือกแท็บ Type และเลือกประเภทสมการของเส้นแนวโน้มแบบโพลิโนเมียล (Polynomial) กำลัง (Order) 2, 3, 4, 5 หรือ 6 ที่เหมาะสมกับชุดข้อมูล ในที่นี้เลือกโพลิโนเมียลกำลัง 5 ตามรูปที่ 9

รูปที่ 9 เลือกประเภทสมการของเส้นแนวโน้ม

- เลือกแท็บ Option และเลือก

Set Intercept  = 0

Display equation on chart

Display R-squared value on chart

คลิก OK ตามรูปที 10

รูปที่ 10 กำหนดรายละเอียดของสมการเส้นแนวโน้ม

จะได้เส้นแนวโน้มแบบโพลิโนเมียล  ซึ่งผ่านจุด (0,0) พร้อมทั้งสมการของเส้นแนวโน้มดังรูปที่ 11

รูปที่ 11 Load-Penetration Curve พร้อมสมการเส้นแนวโน้ม

2.3 การคำนวณหาสมการของเส้นแนวโน้ม

สมการของเส้นแนวโน้มที่แสดงตามรูปที่ 11 นั้น อยู่ในรูปแบบกล่องข้อความ (text box) ซึ่งอาจไม่สะดวกในการคัดลอกไปใช้ในการคำนวณต่อไป รวมทั้งจำนวนเลขนัยสำคัญของสัมประสิทธิ์แต่ละตัวมีค่าน้อย ดังนั้นจะใช้ฟังก์ชัน LINEST ช่วยในการคำนวณค่าสัมประสิทธิ์ของสมการโพลิโนเมียล ดังนี้

- เลือกช่วงเซล D4..I4 ตามรูปที่ 12

รูปที่ 12 การคำนวณค่าสัมประสิทธิ์ของสมการโพลิโนเมียล

- คลิกที่แถบสูตร (Formula bar) พิมพ์

=LINEST(B4:B14,A4:A14^{1,2,3,4,5},FALSE)

โดย  B4:B14 เป็น ชุดข้อมูลของค่า y (Unit Load) จากรูปที่ 4

A4:A14 เป็น ชุดข้อมูลของค่า x (Penetration) จากรูปที่ 4

{ 1, 2, 3, 4, 5 } สำหรับสมการโพลิโนเมียลกำลัง 5 (ถ้าเลือกใช้สมการโพลิโนเมียลกำลัง 3 จะเป็น {1,2,3,})

FALSE เป็น เป็นค่าตรรกะที่ระบุว่าจะกำหนดให้ค่าคงที่ b เท่ากับ 0

กด Control + Shift + Enter จะได้สัมประสิทธิ์ของสมการในเซล D4 ถึง I4 ตามรูปที่ 13

รูปที่ 13 ค่าสัมประสิทธิ์ของสมการโพลิโนเมียลที่คำนวณได้

2.4 คำนวณหาจุดบนกราฟของสมการ y = f(x) ที่มีค่าความชันมากที่สุด

จุดบนกราฟของสมการ y = f(x) ที่มีค่าความชันมากที่สุด คือจุดที่อนุพันธ์อันดับที่หนึ่ง (First Derivative, f’(x)) ของฟังก์ชันมีค่ามากที่สุด ซึ่งในที่นี้จะใช้วิธีการประมาณค่า f’(x) ตามวิธีการในรูปที่ 14 (Centered finite-divided difference) โดยแบ่งค่า x ออกเป็นช่วงๆละ 0.001 in. โดยมีขั้นตอนการคำนวณดังต่อไปนี้

รูปที่ 14 วิธีการประมาณค่า f’(x_i)

(3)

รูปที่ 15 ตั้งชื่อสัมประสิทธิ์ของสมการเส้นแนวโน้มในเซล D4 ถึง H4

รูปที่ 16 การคำนวณค่าอนุพันธ์อันดับที่ 1 ที่จุดต่างๆ

(1) ตั้งชื่อสัมประสิทธิ์ของสมการในเซล D4 เป็น m_1, E4 เป็น m_2, F4 เป็น m_3, G4 เป็น m_4, H4 เป็น m_5 ตามลำดับ ตามรูปที่ 15

(2) ใส่ค่า 1 – 201 ในเซล K4 ถึง เซล K204 ตามรูปที่ 16

(3) ใส่ค่า 0.000 ในเซล L4 และเพิ่มค่าขึ้นครั้งละ 0.001 จนมีค่าเป็น 0.200 ในเซล L204 ตามรูปที่ 16 (จาก Load-Penetration Curve ในรูปที่ 11 จะเห็นได้ว่าจุดที่กราฟมีความชันสูงสุดนั้น ค่า Penetration จะมีค่าไม่เกิน 0.200 นิ้ว)

(4) เลือกเซล M5 เพื่อคำนวณค่า f(x) โดยพิมพ์สูตร

=m_1*L5^5+m_2*L5^4+m_3*L5^3+m_4*L5^2+m_5*L5 จะได้ผลลัพธ์เป็น -0.05 ตามรูปที่ 16

(5) คัดลอกเซล M5 ไปที่เซล M6 ถึง เซล M204 ตามรูปที่ 16

(6) คำนวณค่า f’(x) ตามสมการ

โดยเลือกเซล N5 พิมพ์สูตร = (M6-M4)/0.002 จะได้ผลลัพธ์เป็น -48.99 ตามรูปที่ 16

(7) คัดลอกเซล N5 ไปที่เซล N6 ถึง เซล M203 ตามรูปที่ 16 จะได้ค่า f’(x) ที่ค่า x ต่างๆ

(8) หาค่าความชันสูงสุด โดยเลือกเซล N206 พิมพ์สูตร

=MAX(N5:N203) จะได้ค่าความชันสูงสุดเป็น 406.66 ตามรูปที่ 16

(9) หาตำแหน่งแถวในตารางข้อมูลที่มีค่าความชันสูงสุด ตามที่คำนวณได้ในข้อ (8) โดยเลือกเซล K206 พิมพ์สูตร

=MATCH(N206,N4:N204,0) จะได้ว่าแถวที่ 96 เป็นแถวที่มีค่าความชันสูงสุดในตารางข้อมูล ตามรูปที่ 16

(10) ให้ (x_t,y_t) เป็นจุดที่มีค่าความชันสูงสุด ตามที่คำนวณได้ในข้อ (8)

หาค่า x_t โดยเลือกเซล L206 พิมพ์สูตร

=INDEX(L4:L204,K206) จะได้ผลลัพธ์เป็น 0.095 ซึ่งเท่ากับค่า x ของแถวที่ 96 ตามรูปที่ 16

หาค่า y_t โดยเลือกเซล M206 พิมพ์สูตร

=INDEX(M4:M204,K206) จะได้ผลลัพธ์เป็น 25.32 ซึ่งเท่ากับค่า f(x) ของแถวที่ 96 ตามรูปที่ 16

(11) ดังนั้น จุดบนกราฟของสมการ y = f(x) ที่มีค่าความชันมากที่สุด

ค่าความชัน = 406.66 psi/in

Penetration, x_t =             0.095                     in

Unit Load, y_t =             25.32                      psi

2.5 การคำนวณค่า CBR

คำนวณค่าต่างๆ ที่อ้างถึงตามรูปที่ 17  โดยป้อนสูตรในเซลต่างๆ ตามรูปที่ 18  ดังต่อไปนี้

รูปที่ 17 การคำนวณค่า Δx, x_o

รูปที่ 18 การคำนวณค่าต่างๆและ CBR

นำค่าต่างๆ ที่คำนวณได้อ้างตามรูปที่ 18  ไปพล็อตกราฟได้ตามรูปที่ 19

รูปที่ 19 Load-Penetration Curve ที่ปรับแก้แล้ว

รูปที่ 20 Dry Density vs CBR (ASTM D 1883)

3. สรุป

วิธีการคำนวณปรับแก้ Load-Penetration Curve ตามที่ได้แสดงมาแล้วนั้น มีขั้นตอนการคำนวณมากพอสมควร แต่สามารถทำให้สะดวกในการใช้งานได้โดยเขียนโปรแกรมเพิ่มเติมในบางส่วนด้วย VBA (Visual Basic for Applications) ซึ่งมีอยู่แล้วในโปรแกรม Microsoft Excel

อนึ่ง ในการคำนวณผลการทดสอบ CBR นอกเหนือจาก Load-Penetration Curve แล้ว ยังจะต้องพล็อตกราฟ Dry Density vs CBR (รูปที่ 20) ซึ่งสามารถใช้วิธีการประมาณค่าในช่วงด้วยวิธีผลต่างจากการแบ่งย่อยของนิวตัน (Newton’s divided-difference Interpolating Polynomials) ในการพล็อตกราฟและคำนวณค่าที่ต้องการอ่านจากกราฟ ตามตัวอย่างในบทความ “เทคนิคการใช้โปรแกรม Microsoft Excel คำนวณผลการทดสอบการบดอัดดิน (Compaction Test)”

********************************************

เอกสารอ้างอิง

ปราโมทย์ เดชะอำไพ. (2549). ระเบียบวิธีเชิงตัวเลขในงานวิศวกรรม. พิมพ์ครั้งที่ 5. กรุงเทพฯ: สำนักพิมพ์จุฬาลงกรณ์มหาวิทยาลัย.

วรากร  ไม้เรียง, จิรพัฒน์ โชติกไกร และ ประทีป ดวงเดือน. (2525) ปฐพีกลศาสตร์ ทฤษฎีและปฏิบัติการ. กรุงเทพฯ: ฟิสิกส์เซ็นเตอร์การพิมพ์.

สถาพร คูวิจิตรจารุ. (2541). ทดลองปฐพีกลศาสตร์. กรุงเทพฯ :ไลบราลี ไนน์.

สถาพร คูวิจิตรจารุ. (2542). ปฐพีกลศาสตร์. กรุงเทพฯ :ไลบราลี ไนน์พับลิชชิ่ง.

American Association of State Highway and Transportation Officials. (2003). Standard specification for transportation materials and methods of sampling and testing Part2A:Tests. (23rd Ed).  Washington, D.C.: AASHTO.

American Society for Testing and Materials. (2004). Annual Book of ASTM Standards. Volume 04.08. Soil and Rock (I). Philadelphia, PA : ASTM.

Chapra, S. C. (2008). Applied numerical methods with MATLAB for engineers and scientists. (2nd Ed). Boston: McGraw-Hill Higher Education.