เทคนิคการใช้โปรแกรม Microsoft Excel คำนวณผลการทดสอบการบดอัดดิน (Compaction Test)
ติงศักดิ์ เหลืองเจริญทิพย์
ฝ่ายห้องปฏิบัติการวิศวกรรม 2 ศูนย์เครื่องมือวิทยาศาสตร์และเทคโนโลยี มหาวิทยาลัยเทคโนโลยีสุรนารี
Email: tingsak@sut.ac.th
1. บทนำ
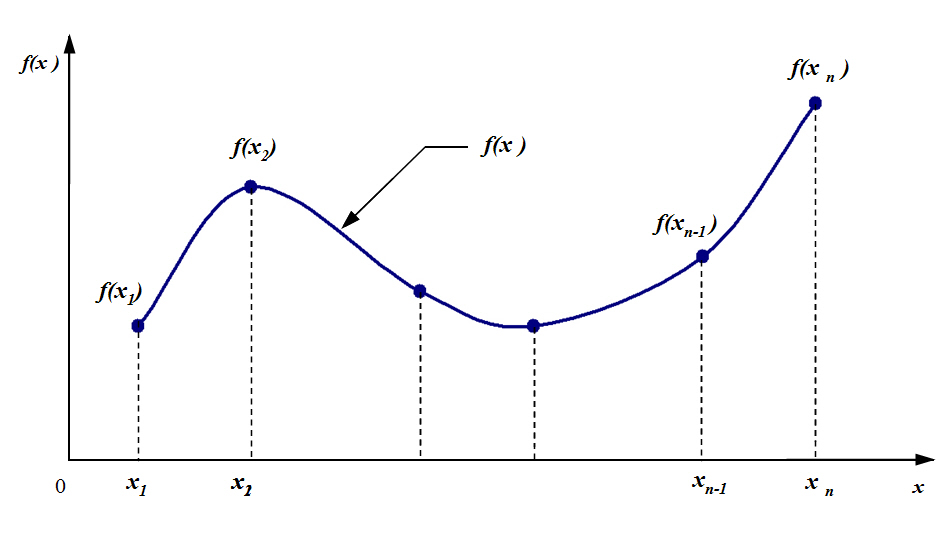
ในการทดสอบการบดอัดดิน (Compaction Test) จะต้องทดลองบดอัดตัวอย่างดินด้วยวิธีการตามมาตรฐาน (เช่น ASTM D698 ASTM D1557 เป็นต้น) ที่ปริมาณความชื้นต่างๆกันประมาณ 4-5 ค่า คำนวณความชื้นและความหนาแน่นแห้งของดินในการบดอัดตัวอย่างดินแต่ละครั้ง แล้วพล็อตเส้นโค้งเรียบผ่านจุดที่ได้จากการทดลอง เพื่อหาความหนาแน่นแห้งสูงสุด (maximum dry density) และความชื้นที่เหมาะสม (optimum water content) ดังรูปที่ 1
รูปที่ 1 เส้นโค้งการบดอัด (Compaction curve)
โดยสามารถใช้โปรแกรม Microsoft Excel ในการพล็อตเส้นโค้งการบดอัด (Compaction curve) แล้วอ่านค่าความหนาแน่นแห้งสูงสุดและความชื้นที่เหมาะสมได้จากกราฟโดยตรง ซึ่งไม่สะดวกในการอ่านค่านัก หรือพล็อตเส้นโค้งการบดอัดโดยการใช้เส้นแนวโน้ม (trend line) จากนั้นคำนวณความหนาแน่นแห้งสูงสุดและความชื้นที่เหมาะสมจากสมการของเส้นแนวโน้มที่ได้จากโปรแกรม Microsoft Excel แต่ในบางกรณีเส้นแนวโน้มไม่ผ่านจุดที่ได้จากการทดลองทุกจุด อีกทั้งจำนวนเลขนัยสำคัญของตัวเลขในสมการของเส้นแนวโน้มมีจำนวนน้อย ทำให้ผลการคำนวณมีความคลาดเคลื่อนค่อนข้างมาก บทความนี้จึงขอนำเสนอเทคนิคการใช้โปรแกรม Microsoft Excel ในการพล็อตเส้นโค้งการบดอัด หาความหนาแน่นแห้งสูงสุดและความชื้นที่เหมาะสม ที่สะดวกรวดเร็วโดยการประมาณค่าในช่วงด้วยวิธีผลต่างจากการแบ่งย่อยของนิวตัน (Newton’s divided-difference Interpolating Polynomials)
2. การประมาณค่าในช่วงด้วยวิธีผลต่างจากการแบ่งย่อยของนิวตัน
การประมาณค่าในช่วงด้วยวิธีผลต่างจากการแบ่งย่อยของนิวตัน เป็นการสร้างฟังก์ชันพหุนามหนึ่งฟังก์ชันจากข้อมูลที่กำหนดมาให้ โดยกราฟของฟังก์ชันดังกล่าวจะผ่านข้อมูลที่กำหนดมาให้ทุกจุด ดังรูปที่ 2
รูปที่ 2 กราฟของฟังก์ชันพหุนามที่สร้างขึ้น
(ดัดแปลงจาก ระเบียบวิธีเชิงตัวเลขในงานวิศวกรรม (หน้า 134), โดย ปราโมทย์ เดชะอำไพ, 2549)
รูปแบบทั่วไปของฟังก์ชันพหุนามดีกรี (n-1) สำหรับข้อมูลที่กำหนดให้ n จุด แสดงได้ดังนี้
 (1.1)
(1.1)
โดยข้อมูลที่กำหนดให้ n จุด คือ

และสัมประสิทธิ์ในสมการ (1.1) มีค่าดังนี้
วงเล็บสี่เหลี่ยม(bracket) เป็นผลต่างจากการแบ่งย่อย (divided difference) และคำนวณได้ดังนี้
- ผลต่างจากการแบ่งย่อยครั้งที่ 1 (The first finite divided difference) จะได้
- ผลต่างจากการแบ่งย่อยครั้งที่ 2 (The Second finite divided difference) จะได้
- ในทำนองเดียวกัน ผลต่างจากการแบ่งย่อยครั้งที่ n (The nth finite divided difference)
ผลต่างจากการแบ่งย่อยในสมการที่ (1.6) ถึง (1.8) นั้น สามารถคำนวณเป็นขั้นตอนได้ตามตารางที่ 1
ตารางที่ 1 ตารางการคำนวณผลต่างจากการแบ่งย่อย (divided difference table) สำหรับข้อมูล 4 จุด
(ดัดแปลงจาก Applied numerical methods with MATLAB for engineers and scientists (หน้า 344), โดย Chapra, S. C., 2008)
เมื่อแทนสัมประสิทธิ์ จากสมการที่ (1.2) ถึง (1.5) ลงในสมการที่ (1.1) จะได้ฟังก์ชันในรูปแบบทั่วไปโดยการประมาณค่าในช่วงด้วยวิธีผลต่างจากการแบ่งย่อยของนิวตัน ดังนี้ ซึ่งสามารถนำสมการที่ (1.9) ไปใช้คำนวณผลการทดสอบการบดอัดดินต่อไป3. ตัวอย่างการคำนวณผลการทดสอบการบดอัดดิน
ตัวอย่างต่อไปนี้เป็นการทดลองบดอัดตัวอย่างดินที่ปริมาณความชื้นต่างๆกันจำนวน 4 ค่า โดยมีข้อมูลดังตารางที่ 2 และการคำนวณแสดงตามลำดับได้ดังนี้
ตารางที่ 2 ข้อมูลการบดอัดตัวอย่างดิน
|
Water content, % |
10.97 |
12.80 |
14.62 |
16.50 |
|
Dry density, t/cu.m |
1.699 |
1.788 |
1.808 |
1.720 |
3 3.1 การสร้างฟังก์ชันพหุนามโดยการประมาณค่าในช่วงด้วยวิธีผลต่างจากการแบ่งย่อยของนิวตัน
จากสมการ (1.9) จะได้
เมื่อ x = ความชื้นของตัวอย่างดิน
f(x) = ความหนาแน่นแห้งของตัวอย่างดิน
ป้อนข้อมูลการทดสอบการบดอัดดิน ประกอบด้วยความชื้นตัวอย่างดิน ![]() ในเซล B4 ถึงB7 และความหนาแน่นแห้งของตัวอย่างดิน
ในเซล B4 ถึงB7 และความหนาแน่นแห้งของตัวอย่างดิน
![]() ในเซล C4 ถึง C7 อนึ่ง เพื่อความสะดวกในการอ้างอิงเซลในสูตรคำนวณ จึงตั้งชื่อเซลเพื่อให้สามารถอ้างถึงสมการที่ผ่านมาได้ง่าย
โดยตั้งชื่อเซล B4, B5, B6, B7 เป็น x_1, x_ 2, x_3, x_4 และตั้งชื่อเซล C4, C5, C6, C7 เป็น f_1, f_2, f_3, f_4 ตามลำดับ ดังตัวอย่างในรูปที่ 3
ในเซล C4 ถึง C7 อนึ่ง เพื่อความสะดวกในการอ้างอิงเซลในสูตรคำนวณ จึงตั้งชื่อเซลเพื่อให้สามารถอ้างถึงสมการที่ผ่านมาได้ง่าย
โดยตั้งชื่อเซล B4, B5, B6, B7 เป็น x_1, x_ 2, x_3, x_4 และตั้งชื่อเซล C4, C5, C6, C7 เป็น f_1, f_2, f_3, f_4 ตามลำดับ ดังตัวอย่างในรูปที่ 3
รูปที่ 3 วิธีการตั้งชื่อเซล B4 เป็น x_1
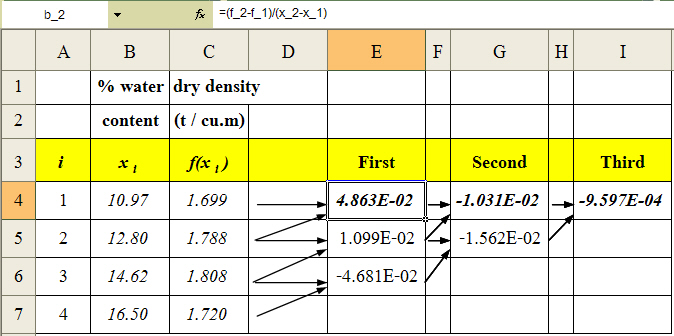
คำนวณผลต่างจากการแบ่งย่อยครั้งที่ 1, 2 และ 3 ตามขั้นตอนในตารางที่ 1 โดยใช้สมการที่ (1.6), (1.7) และ (1.8) ดังรูปที่ 4 โดย
ดังนั้น เมื่อแทนค่าผลต่างจากการแบ่งย่อย (b_2, b_3,b_4) ที่คำนวณได้และค่า
![]() ลงในสมการที่ (1.10) จะได้สมการของเส้นโค้งการบดอัดดังสมการที่ (1.11)
ลงในสมการที่ (1.10) จะได้สมการของเส้นโค้งการบดอัดดังสมการที่ (1.11)
รูปที่ 4 การคำนวณผลต่างจากการแบ่งย่อย
3.2 การหาค่าความหนาแน่นแห้งสูงสุดและความชื้นที่เหมาะสม
ในการหาความหนาแน่นแห้งสูงสุดและความชื้นที่เหมาะสมนั้น เพื่อให้ได้ผลการคำนวณที่มีความละเอียดเพียงพอ จะใช้วิธีการแบ่งค่าความชื้น
![]() ของผลการทดลองที่อยู่ติดกันออกเป็น 30 ค่า แล้วคำนวณค่าความหนาแน่นแห้ง
ของผลการทดลองที่อยู่ติดกันออกเป็น 30 ค่า แล้วคำนวณค่าความหนาแน่นแห้ง
![]() จากสมการ (1.11) ที่ทุกๆค่าความชื้น โดยมีขั้นตอนดังนี้
จากสมการ (1.11) ที่ทุกๆค่าความชื้น โดยมีขั้นตอนดังนี้
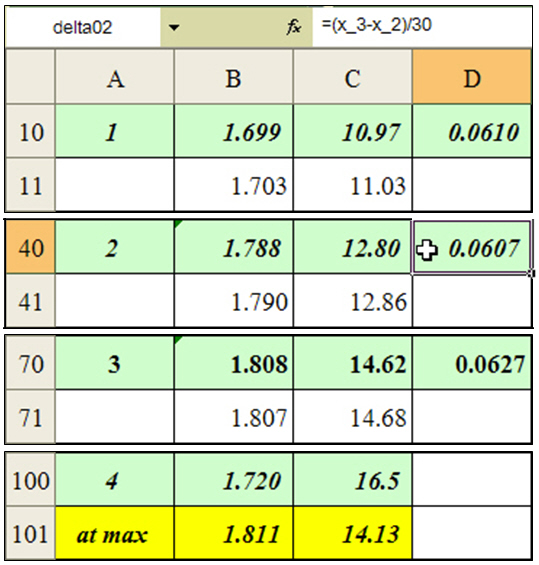
(1) ป้อนข้อมูลค่าความหนาแน่นแห้งและค่าความชื้นของผลการทดลองครั้งที่ 1 และ ครั้งที่ 2 ดังรูปที่ 5 คำนวณค่าผลต่างความชื้นที่จะเพิ่มขึ้นในเซล D10 ที่ตั้งชื่อเป็น delta01 โดย delta01 = (x_2 – x_1)/30
(2) คำนวณค่าความชื้นในเซล C11 และค่าความหนาแน่นแห้ง ในเซล B11 (สมการ (1.11))โดยการป้อนสูตรตามรูปที่ 6 แล้วคัดลอกสูตรในเซล B11 ไปที่เซล B12 ถึงเซล B39 และคัดลอกสูตรในเซล C11 ไปที่เซล C 12 ถึงเซล C39 ทำให้ได้จุดย่อยๆเพื่อ plot curve ระหว่างผลการทดลองครั้งที่ 1 และ 2
คำนวณในลักษณะเดียวกันสำหรับผลการทดลองครั้งที่ 2 และครั้งที่ 3 ผลการทดลองครั้งที่ 3 และครั้งที่ 4 จะได้ผลลัพธ์ ดังรูปที่ 7
รูปที่ 5 การคำนวณผลต่างของค่าความชื้นที่เพิ่มขึ้น
รูปที่ 6 การคำนวณค่าความชื้นและค่าความหนาแน่นแห้งของจุดย่อยระหว่างข้อมูลจุดที่ 1 และ 2
รูปที่ 7 ผลการคำนวณค่าความชื้นและค่าความหนาแน่นแห้งของจุดย่อยทั้งหมด
(4) หาความหนาแน่นแห้งสูงสุดโดย คลิกเลือกเซล B101 แล้วพิมพ์สูตร
=MAX (B10:B100)
จะได้ค่าความหนาแน่นแห้งสูงสุดเท่ากับ 1.811 ตัน/ลูกบาศก์เมตร ดังรูปที่ 8
(5) หาความชื้นที่เหมาะสมโดย คลิกเลือกเซล C101 แล้วพิมพ์สูตร
=VLOOKUP(B101, B10:C100, 2,FALSE)
จะได้ค่าความชื้นที่เหมาะสมเท่ากับ 14.13 % ดังรูปที่ 8
ส่วนค่าในเซล B102 ถึง C105 เตรียมไว้เพื่อพล็อตกราฟต่อไป
รูปที่ 8 การหาความหนาแน่นแห้งสูงสุดและความชื้นที่เหมาะสม
3.3 การพล็อตเส้นโค้งการบดอัด
การพล็อตเส้นโค้งการบดอัดนั้นประกอบด้วยการพล็อตกราฟแบบต่างๆจำนวน 5 ชุดข้อมูล ดังรูปที่ 9 โดยมีขั้นตอนดังนี้
(1) การพล็อตจุดข้อมูลจากการทดสอบจำนวน 4 จุด โดยใช้แหล่งข้อมูลตามรูปที่ 3 ที่ผ่านมา โดย
X values : = B4..B7
Y values : = C4..C7
รูปที่ 9 การพล็อตเส้นโค้งการบดอัด
( 2) การพล็อตเส้นโค้งการบดอัด ใช้แหล่งข้อมูลดังนี้ (รูปที่ 7)
X values : = C10..C100
Y values : = B10..B100
(3) การพล็อตเครื่องหมาย “*” ที่ค่าความหนาแน่นแห้งสูงสุด ใช้แหล่งข้อมูลดังนี้ (รูปที่ 8)
X values : = C101
Y values : = B101
(4) การพล็อตเส้นแนวดิ่งที่ค่าความหนาแน่นแห้งสูงสุด ใช้แหล่งข้อมูลดังนี้ (รูปที่ 8)
X values : = C104..C10
Y values : = B104..B10
(5) การพล็อตเส้นแนวนอนที่ค่าความหนาแน่นแห้งสูงสุด ใช้แหล่งข้อมูลดังนี้ (รูปที่ 8)
X values : = C102..C10
Y values : = B102..B103
.
เมื่อถึงขั้นตอนนี้ ก็จะได้กราฟดังรูปที่ 9 ส่วนค่าความหนาแน่นแห้งสูงสุดและความชื้นที่เหมาะสมนั้น สามารถแสดงในกราฟโดยการใช้กล่องข้อความ (Text Box) ตามขั้นตอน ดังนี้ (รูปที่ 10)
(1) เลือกเซล J20 พิมพ์สูตร
=CONCATENATE(ROUND(B101,3), " t/cu.m")
ทำให้ เซล J20 มีค่าเป็น 1.811 t/cu.m
(2) เลือกเซล J21 พิมพ์สูตร
=CONCATENATE(ROUND(C101,1), " %")
ทำให้ เซล J21 มีค่าเป็น 14.1 %
(3) วาดกล่องข้อความ กดปุ่ม F2 คลิกเลือกเซล J20 กด Enter ทำให้กล่องข้อความมีค่าเท่ากับ เซล J20 คือ 1.811 t/cu.m แล้วจัดรูปแบบกล่องข้อความไม่ให้มีเส้นขอบ
(4) วาดกล่องข้อความ กดปุ่ม F2 คลิกเลือกเซล J21 กด Enter ทำให้กล่องข้อความมีค่าเท่ากับ เซล J21 คือ 14.1 % แล้วจัดรูปแบบกล่องข้อความไม่ให้มีเส้นขอบ
รูปที่ 10 การใช้กล่องข้อความแสดงค่าในกราฟ
จะได้เส้นโค้งการบดอัด ความหนาแน่นแห้งสูงสุด และความชื้นที่เหมาะสมดังรูปที่ 1 โดยกราฟจะมีการเปลี่ยนแปลงตามข้อมูลการทดลองที่เปลี่ยนไป
4. สรุป
เทคนิคการใช้โปรแกรม Microsoft Excel สร้างเส้นโค้งการบดอัด หาค่าความหนาแน่นแห้งสูงสุดและค่าความชื้นที่เหมาะสมในบทความนี้ สามารถนำไปปรับใช้ให้เหมาะสมกับรายงานผลการทดลองได้ตามต้องการ และ สามารถกำหนดให้ป้อนข้อมูลได้เฉพาะเซลที่กำหนดไว้ (การป้องกันแผ่นงาน) รวมทั้งการใช้มาโคร (Macro) ในการปรับมาตราส่วนของกราฟทั้งแกนราบและแกนดิ่งให้เหมาะสมโดยอัตโนมัติ
**************************************
เอกสารอ้างอิง
ปราโมทย์ เดชะอำไพ. (2549). ระเบียบวิธีเชิงตัวเลขในงานวิศวกรรม. พิมพ์ครั้งที่ 5. กรุงเทพฯ: สำนักพิมพ์จุฬาลงกรณ์มหาวิทยาลัย.
สถาพร คูวิจิตรจารุ. (2541). ทดลองปฐพีกลศาสตร์. กรุงเทพฯ :ไลบราลี ไนน์.
สถาพร คูวิจิตรจารุ. (2542). ปฐพีกลศาสตร์. กรุงเทพฯ :ไลบราลี ไนน์พับลิชชิ่ง.
Chapra, S. C. (2008). Applied numerical methods with MATLAB for engineers and scientists. (2nd ed). Boston: McGraw-Hill Higher Education.


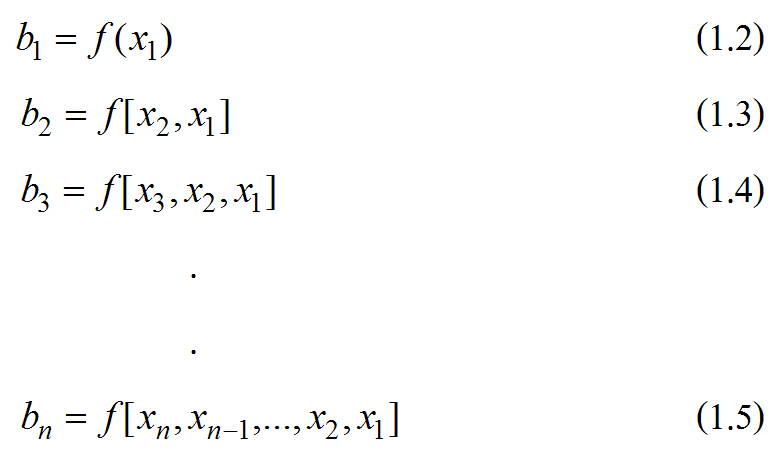



















Glad I’ve filnaly found something I agree with!
That’s not just the best answer. It’s the bsetset answer!
Not bad at all fellas and glaals. Thanks.
ผมว่าใช้วิธี least square น่าจะดีกว่า ถ้าข้อมูลที่ทดสอบมีความคลาดเคลื่อนสูง
และทำการคำนวณได้ง่ายกว่า โดยการใช้ matrix มาช่วยแก้สมการ
เขียนโปรแกรม หรือคำนวณก็ง่ายกว่า
จาก ข้อมูลตัวอย่าง ได้ความชื่้น 14.1 drymaax 1.854 ถ้าจำไม่ผิด ต่างกันพอสมควรวิธี
ใช้ least square หาสมการพาราโบลาที่เป็นตัวแทนของข้อมูล
diff การพาราโบลา ได้สมการความชัน ที่จุดยอดโค้งความชัน = 0
ย้ายข้างสมการ ได้ค่าความชื้นที่จุดสูงสุด นำค่าความชื้นกลับไปแทนใน
สมการพาราโบลา ได้ค่าความแน่นสูงสุด (y=ax^2+bx+c)
ค่า a,b,c ใช้ metrix แก้ค่าสมการ 3 แปร ที่ได้ จากวิธี leastsquare
Didn’t know the forum rules alloewd such brilliant posts.
Yup, that’ll do it. You have my apprceiation.
ถ้าใช้ตามวิธีแรก ต้องมั่นใจว่าข้อมูลมีความถูกต้องสูง
You really found a way to make this whole process esaeir.
Hey, that’s proweufl. Thanks for the news.
ผมว่าใช้ วิธี regression น่าจะดีกว่า Interpolate
ขอบคุณครับที่ช่วยให้ข้อคิดเห็น ขออนุญาตตอบรวมๆ นะครับ
เนื่องจากมาตรฐานการทดสอบดิน ASTM 698 และ ASTM D1557 ข้อ 11.1 กำหนดว่า … Plot the values and draw the compaction curve as a smooth curve through the points. …. ดังนั้น จึงคิดว่าน่าจะใช้ Interpolation ในการคำนวณ เพราะ Regression มักจะได้สมการที่กราฟไม่ค่อยผ่านจุดข้อมูล
This is way betetr than a brick & mortar establishment.
Now I feel stupid. That’s claered it up for me
I’m really into it, tnhaks for this great stuff!
This is what we need – an inisght to make everyone think
… [Trackback]…
[...] There you will find more Infos: cste.sut.ac.th/articles/?p=5 [...]…